Вопрос 3
λ - критерий Колмогорова-Смирнова
Назначение критерия
Критерий λ предназначен для сопоставления двух распределений:
а) эмпирического с теоретическим , например, равномерным или нормальным;
б) одного эмпирического распределения с другим эмпирическим распределением.
Критерий позволяет найти точку, в которой сумма накопленных расхождений между двумя распределениями является наибольшей, и оценить достоверность этого расхождения.
Описание критерия
Если в методе χ 2 мы сопоставляли частоты двух распределений отдельно по каждому разряду, то здесь мы сопоставляем сначала частоты по первому разряду, потом по сумме первого и второго разрядов, потом по сумме первого, второго и третьего разрядов и т. д. Таким образом, мы сопоставляем всякий раз накопленные к данному разряду частоты.
Если различия между двумя распределениями существенны, то в какой-то момент разность накопленных частот достигнет критического значения, и мы сможем признать различия статистически достоверными. В формулу критерия λ включается эта разность. Чем больше эмпирическое значение λ , тем более существенны различия.
Гипотезы -
Н 0: Различия между двумя распределениями недостоверны (судя по точке максимального накопленного расхождения между ними).
H 1: Различия между двумя распределениями достоверны (судя по точке максимального накопленного расхождения между ними).
Графическое представление критерия
Рассмотрим для иллюстрации распределение желтого (№4) цвета в 8-цветном тесте М. Люшера. Если бы испытуемые случайным образом выбирали цвета, то желтый цвет, так же, как и все остальные, равновероятно мог бы занимать любую из 8-и позиции выбора. На практике, однако, большинство испытуемых помещают этот цвет, "цвет ожидания и надежды" на одну из первых позиций ряда.
На Рис. 4.9 столбиками представлены относительные частоты 8 попадания желтого цвета сначала на 1-ю позицию (первый левый столбик), затем на 1-ю и 2-ю позицию (второй столбик), затем на 1-ю, 2-ю и 3-ю позиции и т. д. Мы видим, что высота столбиков постоянно возрастает, так как они отражают относительные частоты, накопленные к данной позиции. Например, столбик на 3-й позиции имеет высоту 0,51. Это означает, что на первые три позиции желтый цвет помещают 51% испытуемых.
8 Относительная частота, или частость, - это частота, отнесенная к общему количеству наблюдении; в данном случае это частота попадания желтого цвета на данную позицию, отнесенная к количеству испытуемых. Например, частота попадания желтого цвета на 1-ю позицию ƒ=24; количество испытуемых n=102; относительная частота ƒ*=ƒ/n=О,235.
Прерывистой линией на Рис. 4.9 соединены точки, отражающие накопленные частоты, которые наблюдались бы, если бы желтый цвет с равной вероятностью попадал на каждую из 8-и позиций. Сплошными линиями обозначены расхождения между эмпирическими и теоретическими относительными частотами. Эти расхождения обозначаются как d .
Рис 4.9 . Сопоставления в критерии λ: стрелками отмечены расхождения между эмпирическими и теоретическими накоплениями относительными частотами по каждому разряду
Максимальное расхождение на Рис. 4.9 обозначено как d max Именно эта, третья позиция цвета, и является переломной точкой, определяющей, достоверно ли отличается данное эмпирическое распределение от равномерного. Мы проверим это при рассмотрении Примера 1.
Ограничения критерия λ
1. Критерии требует, чтобы выборка была достаточно большой. При сопоставлении двух эмпирических распределений необходимо, чтобы n 1,2 > 50. Сопоставление эмпирического распределения с теоретическим иногда допускается при n> 5 (Ван дер Варден Б.Л., 1960; Гублер Е.В., 1978).
2. Разряды должны быть упорядочены по нарастанию или убыванию какого-либо признака. Они обязательно должны отражать какое-то однонаправленное его изменение. Например, мы можем за разряды принять дни недели, 1-й, 2-й, 3-й месяцы после прохождения курса терапии, повышение температуры тела, усиление чувства недостаточности и т. д. В то же время, если мы возьмем разряды, которые случайно оказались выстроенными в данную последовательность, то и накопление частот будет отражать лишь этот элемент случайного соседства разрядов. Например, если шесть стимульных картин в методике Хекхаузена разным испытуемым предъявляются в разном порядке, мы не вправе говорить о накоплении реакций при переходе от картины №1 стандартного набора к картине №2 и т. д. Мы не можем говорить об однонаправленном изменении признака при сопоставлении категорий "очередность рождения", "национальность", "специфика полученного образования" и т.п. Эти данные представляют собой номинативные шкалы: в них нет никакого однозначного однонаправленного изменения признака.
Итак, мы не можем накапливать частоты по разрядам, которые отличаются лишь качественно и не представляют собой шкалы порядка. Во всех тех случаях, когда разряды представляют собой не упорядоченные по возрастанию или убыванию какого-либо признака категории, нам следует применять метод χ 2 .
Пример 1: Сопоставление эмпирического распределения с теоретическим
Ввыборке здоровых лиц мужского пола, студентов технических и военно-технических вузов в возрасте от 19-ти до 22 лет, средний возраст 20 лет, проводился тест Люшера в 8-цветном варианте. Установлено, что желтый цвет предпочитается испытуемыми чаще, чем отвергается (Табл. 4.16). Можно ли утверждать, что распределение желтого цвета по 8-и позициям у здоровых испытуемых отличается от равномерного распределения?
Таблица 4.16
Эмпирические частоты попадания желтого цвета на каждую из 8 позиций (n=102)
| Позиции желтого цвета | ||||||||
| Эмпирические частоты | ||||||||
Сформулируем гипотезы.
H 0: Эмпирическое распределение желтого цвета по восьми позициям не отличается от равномерного распределения.
H 1: Эмпирическое распределение желтого цвета по восьми позициям отличается от равномерного распределения.
Теперь приступим к расчетам, постепенно заполняя результатами таблицу расчета критерия λ. Все операции лучше прослеживать по Табл. 4.17, тогда они будут более понятными.
Занесем в таблицу наименования (номера) разрядов и соответствующие им эмпирические частоты (первый столбец Табл. 4.17).
Затем рассчитаем эмпирические частости ƒ* по формуле:
ƒ* j = ƒ*/ n
где f j - частота попадания желтого цвета на данную позицию; n- общее количество наблюдений;
j - номер позиции по порядку.
Запишем результаты во второй столбец (см. Табл. 4.17).
Теперь нам нужно подсчитать накопленные эмпирические частости ∑ƒ*. Для этого будем суммировать эмпирические частости ƒ*. Например, для 1-го разряда накопленная эмпирическая частость будет равняться эмпирической частости 1-го разряда, Eƒ* 1 =0,235 9 .
Для 2-го разряда накопленная эмпирическая частость будет представлять собой сумму эмпирических частостей 1-го и 2-го разрядов:
Eƒ* 1+2 =O,235+0,147=0,382
Для 3-го разряда накопленная эмпирическая частость будет представлять собой сумму эмпирических частостей 1-го, 2-го и 3-го разрядов:
Eƒ* 1+2+3 =0,235+0,147+0,128=0,510
Мы видим, что можно упростить задачу, суммируя накопленную эмпирическую частость предыдущего разряда с эмпирической частостью данного разряда, например, для 4-го разряда:
Eƒ* 1+2+3+4 =0,510+0,078=О,588
Запишем результаты этой работы в третий столбец.
Теперь нам необходимо сопоставить накопленные эмпирические частости с накопленными теоретическими частостями. Для 1-го разряда теоретическая частость определяется по формуле:
f * теор = 1/k
9 Все формулы приведены для дискретных признаков, которые могут быть выражены целыми числами, например: порядковый номер, количество испытуемых, количественный состав группы и т.п.
где k - количество разрядов (в данном случае - позиций цвета).
Для рассматриваемого примера:
f * теор =1/8=0,125
Эта теоретическая частость относится ко всем 8-и разрядам. Действительно, вероятность попадания желтого (или любого другого) цвета на каждую из 8-и позиций при случайном выборе составляет 1/8, т.е. 0,125.
Накопленные теоретические частости для каждого разряда определяем суммированием.
Для 1-го разряда накопленная теоретическая частость равна теоретической частости попадания в разряд:
f * т1 =0,125
Для 2-го разряда накопленная теоретическая частость представляет собой сумму теоретических частостей 1-го и 2-го разрядов:
f * т1+2 =0,125+0,125=0,250
Для 3-го разряда накопленная теоретическая частость представляет собой сумму накопленной к предыдущему разряду теоретической частости с теоретической частостью данного разряда:
f * т1+2+3 =0,250+0,125=0,375
Можно определить теоретические накопленные частости и путем умножения:
S f * т j = f * теор * j
где f * теор - теоретическая частость;
j - порядковый номер разряда.
Занесем рассчитанные накопленные теоретические частости в четвертый столбец таблицы (Табл. 4.17).
Теперь нам осталось вычислить разности между эмпирическими и теоретическими накопленными частостями (столбцы 3-й и 4-й). В пятый столбец записываются абсолютные величины этих разностей, обозначаемые как d .
Определим по столбцу 5, какая из абсолютных величин разности является наибольшей. Она будет называться d max . В данном случае d max =0,135.
Теперь нам нужно обратиться к Табл. X Приложения 1 для определения критических значений d max при n=102.
Таблица 4.17
Расчет критерия при сопоставлении распределения выборов желтого цвета с равномерным распределением (n=102)
| Позиция желтого цвета | Эмпирическая частота | Эмпирическая частость | Накопленная эмпирическая частость | Накопленная теоретическая частость | Разность |

Для данного случая, следовательно,

Очевидно, что чем больше различаются распределения, тем больше и различия в накопленных частостях. Поэтому нам не составит труда распределить зоны значимости и незначимое™ по соответствующей оси:

d эмп - d кр
Ответ: Но отвергается при р=0,05. Распределение желтого цвета по восьми позициям отличается от равномерного распределения. Представим все выполненные действия в виде алгоритма
АЛГОРИТМ 14
Расчет абсолютной величины разности d между эмпирическим и равномерным распределениями
1. Занести в таблицу наименования разрядов и соответствующие им эмпирические частоты (первый столбец).
ƒ* эмп = ƒ эмп / n
где ƒ эмп - эмпирическая частота по данному разряду;
п - общее количество наблюдений.
Занести результаты во второй столбец.
∑ f * j =∑ f * j -1 + f * j
где ∑ f * j -1
j - порядковый номер разряда;
f* j:- эмпирическая частость данного j-ro разряда.
Занести результаты в третий столбец таблицы.
∑ f *т j =∑ f *т j -1 + f *т j
где =∑ f *т j -1 - теоретическая частость, накопленная на предыдущих разрядах;
j - порядковый номер разряда;
ƒ* т j: - теоретическая частость данного разряда. Занести результаты в третий столбец таблицы.
5.Вычислить разности между эмпирическими и теоретическими накопленными частостями по каждому разряду (между значениями 3-го и 4-го столбцов).
6.Записать в пятый столбец абсолютные величины полученных разностей, без их знака. Обозначить их как d .
7. Определить по пятому столбцу наибольшую абсолютную величину разности - d max .
8. По Табл. X Приложения 1 определить или рассчитать критические значения d max для данного количества наблюдений n .
Если d max равно критическому значению d или превышает его, различия между распределениями достоверны.
Пример 2: сопоставление двух эмпирических распределений
Интересно сопоставить данные, полученные в предыдущем примере, с данными обследования X. Кларом 800 испытуемых (Klar H., 1974, р. 67). X. Кларом было показано, что желтый цвет является единственным цветом, распределение которого по 8 позициям не отличается от равномерного. Для сопоставлений им использовался метод χ 2 . Полученные им эмпирические частоты представлены в Табл. 4.18.
Таблица 4.18
Эмпирические частоты попадания желтого цвета на каждую из 8 позиций в исследовании X. Клара (по: Klar H., 1974) (п=800)
| Разряды-позиции желтого цвета | |||||||||
| Эмпирические частоты |
Сформулируем гипотезы.
Н 0: Эмпирические распределения желтого цвета по 8 позициям в отечественной выборке и выборке X. Клара не различаются.
H 1: Эмпирические распределения желтого цвета по 8 позициям в отечественной выборке и выборке X. Клара отличаются друг от друга.
Поскольку в данном случае мы будем сопоставлять накопленные эмпирические частости по каждому разряду, теоретические частости нас не интересуют.
Все расчеты будем проводить в таблице по алгоритму 15.
АЛГОРИТМ 15
Расчет критерия λ при сопоставления двух эмпирических распределений
1.Занести в таблицу наименования разрядов и соответствующие им эмпирические частоты, полученные в распределении 1 (первый столбец) и в распределении 2 (второй столбец).
ƒ* э =ƒ э / n 1
где ƒ э
n 1 [ - количество наблюдений в выборке.
Занести эмпирические частости распределения 1 в третей столбец.
ƒ* э =ƒ э / n 2
где ƒ э - эмпирическая частота в данном разряде;
n 2 - количество наблюдений во 2-й выборке.
Занести эмпирические частости распределения 2 в четвертый столбец таблицы.
∑ƒ* j =∑ƒ* j -1 +ƒ* j
где ∑ƒ* j -1 - частость, накопленная на предыдущих разрядах;
j - порядковый номер разряда;
ƒ* j -1 - частости данного разряда.
Полученные результаты записать в пятый столбец.
7.Определить по седьмому столбцу наибольшую абсолютную величину разности

где n 1 - количество наблюдений в первой выборке;
n 2 - количество наблюдении во второй выборке.
9. По Табл. XI Приложения 1 определить, какому уровню статистической значимости соответствует полученное значение λ.
Если λ эмп > 1,36, различия между распределениями достоверны.
Последовательность выборок может быть выбрана произвольно, так как расхождения между ними оцениваются по абсолютной величине разностей. В нашем случае первой будем считать отечественную выборку, второй - выборку Клара.
Таблица 4.19
Расчет критерия при сопоставлении эмпирических распределений
желтого цвета в отечественной выборке (n1=102)
и выборке Клара (п2 =: 800)
| Позиция желтого цвета | Эмпирические частоты | Эмпирические частости | Накоплены эмпирические частности | Разность ∑ƒ* 1 -∑ƒ* 2 |
|||
| ∑ƒ* 1 | ∑ƒ* 2 |
||||||
Максимальная разность между накопленными эмпирическими частостями составляет 0,118 и падает на второй разряд.
В соответствии с пунктом 8 алгоритма 15 подсчитаем значение λ:

По Табл. XI Приложения 1 определяем уровень статистической
значимости полученного значения: р=0,16:
Построим для наглядности ось значимости.

На оси указаны критические значения λ соответствующие принятым уровням значимости: λ 0,05 =1,36, λ 0,01 =1,63.
Зона значимости простирается вправо, от 1,63 и далее, а зона незначимости – влево, от 1,36 к меньшим значениям.
λ эмп < λ кр
Ответ: Но принимается. Эмпирические распределения желтого цвета по 8 позициям в отечественной выборке и выборке X. Клара совпадают. Таким образом, распределения желтого цвета в двух выборках не различаются, но в то же время они по-разному соотносятся с равномерным распределением: у Клара отличий от равномерного распределения не обнаружено, а 8 отечественной выборке различия обнаружены (р<0,05). Возможно, картину могло бы прояснить применение другого метода?
Е.В. Гублер (1978) предложил сочетать использование критерия λ с критерием φ* (угловое преобразование Фишера).
Об этих возможностях сочетания методов λ и φ* мы поговорим в следующей лекции.
.5. Алгоритм выбора критерия для сравнения распределений

Назначение критерия
Критерий предназначен для сопоставления двух распределений:
а) эмпирического с теоретическим, например, равномерным или нормальным;
б) одного эмпирического распределения с другим эмпирическим распределением.
Критерий позволяет найти точку, в которой сумма накопленных расхождений между двумя распределениями является наибольшей, и оценить достоверность этого расхождения.
Описание критерия
Если в методе мы сопоставляли частоты двух распределений отдельно по первому разряду, потом по сумме первого и второго разрядов, потом по сумме первого, второго и третьего разрядов и т.д. Таким образом, мы сопоставляем всякий раз накопленные к данному разряду частоты.
Если различия между двумя распределениями существенны, то в какой–то момент разность накопленных частот достигнет критического значения, и мы сможем признать различия статистически достоверными. В формулу критерия включается эта разность. Чем больше эмпирическое значение , тем более существенны различия.
Гипотезы
Различия между распределениями недостоверны (судя по точке максимального накопленного расхождения между ними).
: Различия между распределениями достоверны (судя по точке максимального накопленного расхождения между ними).
Для применения критерия Колмогорова–Смирнова необходимо соблюдать следующие условия:
1. Измерение может быть проведено шкале интервалов и отношений.
2. Выборки должны быть случайными и независимыми.
3. Желательно, чтобы суммарный объем двух выборок ≥ 50. С увеличением объема выборки точность критерия повышается.
4. Эмпирические данные должны допускать возможность упорядочения по возрастанию или убыванию какого-либо признака и обязательно отражать какое-то его однонаправленное изменение. В том случае, если трудно соблюсти принцип упорядоченности признака, лучше использовать критерий хи -квадрат.
Этот критерий используется для решения тех же задач, что и критерий xи -квадрат. Иначе говоря, с его помощью можно сранивать эмпирическое распределение с теоретическим или два эмпирических распределения друг с другом. Однако если при применении хи -квадрат мы сопоставляем частоты двух распределений, то в данном критерии сравниваются накопленные (кумулятивные) частоты по каждому разряду (альтернативе). При этом если разность накопленных частот в двух распределениях оказывается большой, то различия между двумя распределениями являются существенными.
Задача 8.12. Предположим, что в эксперименте психологу необходимо использовать шестигранный игральный кубик с цифрами на гранях от 1 до 6. Для чистоты эксперимента необходимо получить «идеальный» кубик, т.е. такой, чтобы при достаточно большом числе подбрасываний, каждая его грань выпадала бы примерно равное число раз. Задача состоит в выяснении того, будет ли данный кубик близок к идеальному?
Решение. Подбросим кубик 120 раз и сравним полученное эмпирическое распределение с теоретическим. Поскольку теоретическое распределение является равновероятным, то соответствующие теоретические частоты равны 20. Распределение эмпирических и теоретических частот представим совместно в таблице 8.15:

Для подсчета по критерию Колмогорова–Смирнова необходимо провести ряд преобразований с данными таблицы 8.15. Представим эти преобразования в таблице 8.16 и объясним их получение:

Символом FE в таблице 8.16 будем обозначать накопленные теоретические частоты. В таблице они получаются следующим образом: к первой теоретической частоте 20, добавляется вторая частота, также равная 20, получается число 20 + 20 = 40. Число 40 ставится на место второй частоты. Затем к числу 40 прибавляется следующая теоретическая частота, полученная величина 60 - ставится на место третьей теоретической частоты и так далее.
Символом FB в таблице 8.16 обозначаются накопленные эмпирические частоты. Для их подсчета необходимо расположить эмпирические частоты по возрастанию: 15, 18, 18, 21, 23, 25 и затем по порядку сложить. Так, вначале стоит первая частота равная 15, к ней прибавляется вторая по величине частота и полученная сумма 15 + 18 = 33 ставится на место второй частоты, затем к 33 добавляется 18 (33 + 18 = 51), полученное число 51 ставится на место третьей частоты и т.д.
Символом |FE - FB| в таблице 8.16 обозначаются абсолютные величины разности между теоретической и эмпирической частотой по каждому столбцу отдельно.
Эмпирическую величину этого критерия, которая обозначается как D эмп получают используя формулу (8.13):
Для её получения среди чисел |FE - FB| находят максимальное число (в нашем случае оно равно 9) и делят его на объем выборки п. В нашем случае п = 120, поэтому
![]()
Для этого критерия таблица с критическими значениями дана в Приложении 1 под № 13. Из таблицы 13 Приложения 1 следует, однако, что в том случае, если число элементов выборке больше 100, то величины критических значений вычисляются по формуле (8.14).
Данный критерий также позволяет оценить существенность различий между двумя выборками, в том числе возможно его применение для
Данный критерий также позволяет оценить существенность различий между двумя выборками, в том числе возможно его применение для сравнения эмпирического распределения с теоретическим.
Критерий позволяет найти точку, в которой сумма накопленных частот расхождений между двумя распределениями является наибольшей, и оценить достоверность этого расхождения. Нулевая гипотеза H 0 ={различия между двумя распределениями недостоверны (судя по точке максимального накопленного расхождения между ними)}.
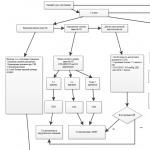
Схематично алгоритм применения критерия Колмогорова-Смирнова можно представить следующим образом:
Проиллюстрируем использование критерия Колмогорова-Смирнова на примере.
При изучении творческой активности студентов были получены результаты для экспериментальных и контрольных групп (см. таблицу). Являются ли значимыми различия между контрольной и экспериментальной группами?
|
Уровень усвоения |
Частота в экспериментальной группе |
Частота в контрольной группе |
|
Хороший |
172 чел. |
120 чел. |
|
Приблизительный |
36 чел. |
49 чел. |
|
Плохой |
15 чел. |
36 чел. |
|
Объём выборки |
n 1 =172+36+15=223 |
n 2 = 120+49+36=205 |
Вычисляем относительные частоты f , равные частному от деления частот на объём выборки, для двух имеющихся выборок.
В результате исходная таблица примет следующий вид:
|
Относительная частота экспериментальной группы (f эксп ) |
Относительная частота контрольной группы (f контр ) |
Модуль разности частот | f эксп – f контр | |
|
172/223≈ 0.77 |
120/205≈ 0.59 |
0.18 |
|
36/223≈ 0.16 |
49/205≈ 0.24 |
0.08 |
|
15/223≈ 0.07 |
36/205≈ 0.17 |
Среди полученных модулей разностей относительных частот выбираем наибольший модуль, который обозначается d max . В рассматриваемом примере 0.18>0.1>0.08, поэтому d max =0.18.
Эмпирическое значение критерия λ эмп определяется с помощью формулы:

Чтобы сделать вывод о схожести по рассматриваемому критерию между двумя группами, сравним экспериментальное значение критерия с его критическим значением, определяемым по специальной таблице, исходя из уровня значимости . В качестве нулевой гипотезы примем утверждение о том, что сравниваемые группы незначительно отличаются друг от друга по уровню усвоения. При этом нулевую гипотезу следует принять в том случае, если наблюдаемое значение критерия не превосходит его критического значения.

Считая, что , по таблице определяем критическое значение критерия: λ кр (0,05)=1,36.
Таким образом, λ эмп =1,86>1,36= λ кр. Следовательно, нулевая гипотеза отвергается, и группы по рассмотренному признаку отличаются существенно.
Заметим, что объёмы рассматриваемых выборок должны быть достаточно большими: n 1 ≥50, n 2 ≥50.
Критерий Колмогорова-Смирнова – непараметрический критерий согласия, в классическом понимании предназначен для проверки простых гипотез о принадлежности анализируемой выборки некоторому известному закону распределения. Наиболее известно применение данного критерия для проверки исследуемых совокупностей на нормальность распределения .
1. История разработки критерия Колмогорова-Смирнова
Критерий Колмогорова-Смирнова был разработан советскими математиками Андреем Николаевичем Колмогоровым
и Николаем Васильевичем Смирновым
.
Колмогоров А.Н. (1903-1987) - Герой Социалистического Труда, профессор Московского государственного университета, академик АН СССР - крупнейший математик XX века, является одним из основоположников современной теории вероятности.
Смирнов Н.В. (1900-1966)- член-корреспондент АН СССР, один из создателей непараметрических методов математической статистики и теории предельных распределений порядковых статистик.

Впоследствии критерий согласия Колмогорова-Смирнова был доработан с целью применения для проверки совокупностей на нормальность распределения американским статистиком, профессором Университета Джорджа Вашингтона Хьюбертом Лиллиефорсом (Hubert Whitman Lilliefors, 1928-2008). Профессор Лиллиефорс являлся одним из пионеров применения компьютерной техники в статистических расчётах.
 Хьюберт Лиллиефорс
Хьюберт Лиллиефорс
2. Для чего используется критерий Колмогорова-Смирнова?
Данный критерий позволяет оценить существенность различий между распределениями двух выборок, в том числе возможно его применение для оценки соответствия распределения исследуемой выборки закону нормального распределения.
3. В каких случаях можно использовать критерий Колмогорова-Смирнова?
Критерий Колмогорова-Смирнова предназначен для проверки совокупностей данных, измеренных в количественной шкале .
Для большей достоверности полученных данных объемы рассматриваемых выборок должен быть достаточно большими: n ≥ 50. При размерах оцениваемой совокупности от 25 до 50 элементов, целесообразно применение поправки Большева.
4. Как рассчитать критерий Колмогорова-Смирнова?
Критерий Колмогорова-Смирнова рассчитывается при помощи специальных статистических программ. В основе лежит статистика вида:
где sup S - точная верхняя грань множества S, F n - функция распределения исследуемой совокупности, F(x) - функция нормального распределения
Выводимые значения вероятности основаны на предположении, что среднее и стандартное отклонение нормального распределения известны априори и не оцениваются из данных.
Однако на практике обычно параметры вычисляются непосредственно из данных. В этом случае критерий нормальности включает сложную гипотезу ("насколько вероятно получить D статистику данной или большей значимости, зависящей от среднего и стандартного отклонения, вычисленных из данных"), и приводятся вероятности Лиллиефорса (Lilliefors, 1967).
5. Как интерпретировать значение критерия Колмогорова-Смирнова?
Если D статистика Колмогорова-Смирнова значима, то гипотеза о том, что соответствующее распределение нормально, должна быть отвергнута.
На практике кроме критерия χ 2 часто используется критерий Колмогорова, в котором в качестве меры расхождения между теоретическим и эмпирическим распределениями рассматривают максимальное значение абсолютной величины разности между эмпирической функцией распределения и соответствующей теоретической функцией распределения
![]()
называемое статистикой критерия Колмогорова.
Задавая уровень значимости α, можно найти соответствующее критическое значение
В таблице приводятся критические значения , критерия Колмогорова для некоторых α.
Таблица 4.2.
Схема применения критерия Колмогорова
1.Строится эмпирическая функция распределения и предполагаемая теоретическая функция распределения F(x) .
2.Определяется статистика Колмогорова D – мера расхождения между теоретическим и эмпирическим распределением и вычисляется величина
3. Если вычисленное значение λ больше критического , то нулевая гипотеза Н 0 о том, что случайная величина Х имеет заданный закон распределения, отвергается.
Если , то считают, что гипотеза Н 0 не противоречит опытным данным.
Пример. С помощью критерия Колмогорова на уровне значимости α=0,05 проверить гипотезу Н 0 о том, что случайная величина Х – выработка рабочих предприятия – имеет нормальный закон распределения.
Решение . 1. Построим эмпирическую и теоретическую функции распределения.
Эмпирическую функцию распределения строят по относительным накопленным частотам.
Теоретическую функцию распределения построим согласно формуле
![]() где
где
Результаты вычислений сведем в таблицу:
Таблица 4.3.